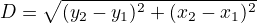Table of Contents
Midpoint between two points
Be 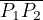 defined by
defined by 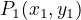 and
and 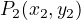
Midpoint 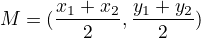
slope straight line
points 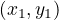 and
and 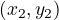
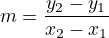
slope intercept form
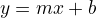
find line equation
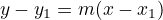
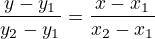
distance between two points
Using Pythagoras' Theorem: The distance(D) between two points 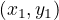 and
and 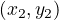 is given by:
is given by: 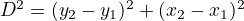 so
so